пузырьком, выбором, кучей, вставками, слиянием и быстрая
Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
Интересно, хочу попробовать
Все любят, когда данные отсортированы. Сортировка позволяет упорядочивать данные в нужной нам последовательности. В порядке возрастания и убывания. Представьте, что вы работаете в крупной компании и вам нужно отсортировать имена работников в зависимости от их зарплаты. Для этого используются алгоритмы сортировки.
Сегодня мы рассмотрим основные виды алгоритмов сортировки. Но сперва проясним, что из себя представляет сортировочный алгоритм.
Что такое алгоритм сортировки?
Сортировка больших объемов данных отнимает много сил и времени. Алгоритмы сортировки, как упоминалось ранее, позволяют облегчить выполнение этой задачи.
Алгоритмы сортировки позволяют упорядочить заданные списки и массивы данных с помощью операторов сравнения. Эти операторы применяются к элементам массива и определяют их последовательность в структуре данных.
К примеру, символы ниже идут в порядке возрастания согласно кодировке ASCII. В процессе сортировки идет сравнение элементов между собой. Чем выше значение символа в таблице ASCII, тем дальше от начала списка он будет расположен.
Какие существуют алгоритмы сортировки?
Существует множество различных алгоритмов. Сегодня мы рассмотрим 6 из них.
Сегодня мы рассмотрим 6 из них.
| Сортировка пузырьком | Один из простейших методов сортировки. Заключается в постепенном смещении элементов с большим значением в конец массива. Элементы последовательно сравниваются попарно, и если порядок в паре нарушен – меняются местами. |
| Сортировка выбором | Алгоритм ищет наименьший элемент в текущем списке и производит обмен его значения со значением первой неотсортированной позиции. То же самое происходит со вторым элементом с наименьшим значением. Цикл повторяется до тех пор, пока все элементы не займут нужную последовательность. |
| Быстрая сортировка | Считается одним из самых быстрых алгоритмов сортировки. Как и сортировка слиянием, работает по принципу «разделяй и властвуй». Временная сложность алгоритма может достигать O(n log n).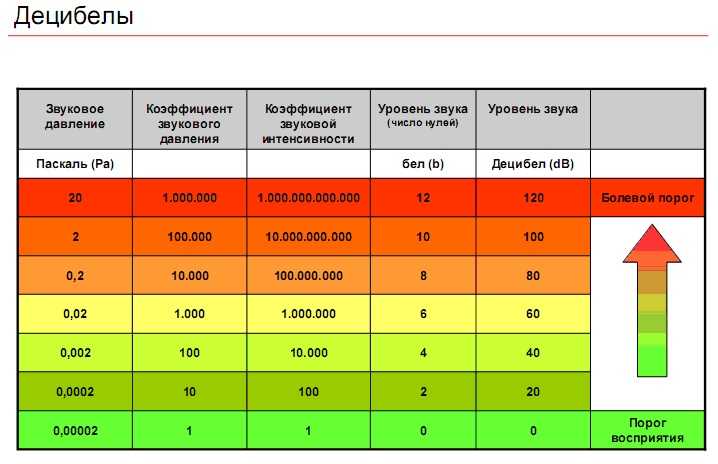 |
| Сортировка кучей (Пирамидальная сортировка) | Алгоритм выстраивает данные в виде двоичного дерева (двоичной кучи). Существует два варианта расположения элементов – max-heap (значение родителя больше значений потомков) и min-heap (значение родителя меньше значений потомков). Наибольший / наименьший элемент (в зависимости от типа) располагается в корне дерева. Он меняется местами с последним элементом кучи и помещается в конец массива. Размер кучи уменьшается на 1, после чего она перестраивается. Цикл повторяется, пока размер кучи больше 1. |
| Сортировка вставками | Применяется для вставки элементов массива на «свое место». Сортировка вставками представляет собой простой метод сортировки и используется для раскладки колоды во время игры в бридж. |
| Сортировка слиянием | Следует принципу «разделяй и властвуй», согласно которому массив данных разделяется на равные части, которые сортируются по-отдельности.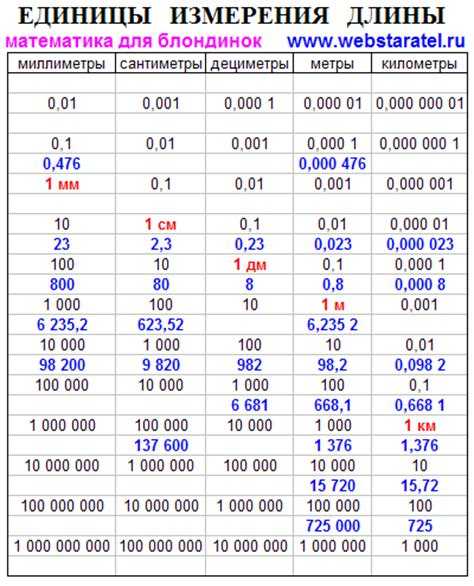 После они сливаются, в результате получается отсортированный массив. После они сливаются, в результате получается отсортированный массив. |
Сортировка, в результате которой относительная последовательность элементов не изменилась, называется устойчивой.
При неустойчивой сортировке элементы в массиве меняются местами.
Какие алгоритмы сортировки обеспечивают стабильность?
В таблице ниже представлена стабильность рассмотренных алгоритмов сортировки
| Алгоритм сортировки | Стабильность |
| Сортировка пузырьком | ✓ |
| Сортировка выбором | ✘ |
| Быстрая сортировка | ✘ |
| Сортировка кучей | ✘ |
| Сортировка вставками | ✓ |
| Сортировка слиянием | ✓ |
Можно ли оценить эффективность алгоритмов сортировки?
Да, это возможно.
Критериями оценки эффективности алгоритма сортировки является пространственная и временная сложность.
Пространственная сложность
Означает количество памяти, затраченной на выполнение алгоритма. Пространственная сложность включает вспомогательную память и память для хранения входных данных.
Вспомогательная память – дополнительное место, занимаемое алгоритмом помимо входных данных. Она учитывается при расчете пространственной сложности алгоритмов.
Временная сложность
Означает время, за которое алгоритм выполняет поставленную задачу с учетом входных данных. Может быть выражена с использованием следующих нотаций:
- Нотация «Омега» (Ω)
- Нотация «O» большое (O)
- Нотация «Тета» (Θ)
В таблице представлена оценка сложности алгоритмов, упомянутых ранее
| Алгоритм сортировки | Время работы в худшем случае | Время работы в среднем случае | Время работы в лучшем случае | Пространственная сложность |
| Сортировка пузырьком | n^2 | n^2 | n | 1 |
| Сортировка выбором | n^2 | n^2 | n^2 | 1 |
| Быстрая сортировка | n^2 | nlog n | nlog n | nlog n |
| Сортировка кучей | nlog n | nlog n | nlog n | 1 |
| Сортировка вставками | n^2 | n^2 | n | 1 |
| Сортировка слиянием | nlog n | nlog n | nlog n | n |
***
У каждого алгоритма сортировки своя временная и пространственная сложность. Использовать можно любой из представленных алгоритмов в зависимости от поставленных задач. Но по моему субъективному мнению лучшим алгоритмом является быстрая сортировка. Она позволяет выбрать опорный элемент и разделяет массив на 3 части: меньше, равно и больше опорного элемента.
Использовать можно любой из представленных алгоритмов в зависимости от поставленных задач. Но по моему субъективному мнению лучшим алгоритмом является быстрая сортировка. Она позволяет выбрать опорный элемент и разделяет массив на 3 части: меньше, равно и больше опорного элемента.
Больше полезной информации вы можете найти на нашем телеграм-канале «Библиотека программиста»
Интересно, перейти к каналу
Материалы по теме
- ☕ Разбираемся в алгоритме быстрой сортировки с помощью JavaScript
- 👨🎓️ Алгоритмы и структуры данных на C++ для новичков. Часть 1: Основы анализа алгоритмов
- ☕ Распространенные алгоритмы и структуры данных в JavaScript: полезные алгоритмы для веб-разработки
Поиск отличий в двух списках
28591
06.11.2012
Скачать пример
Типовая задача, возникающая периодически перед каждым пользователем Excel — сравнить между собой два диапазона с данными и найти различия между ними.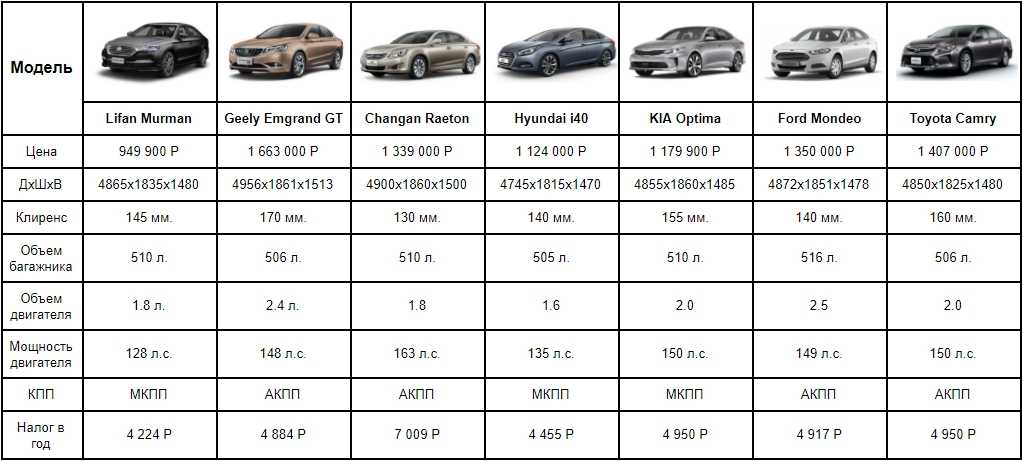 Способ решения, в данном случае, определяется типом исходных данных.
Способ решения, в данном случае, определяется типом исходных данных.
Вариант 1. Синхронные списки
Если списки синхронизированы (отсортированы), то все делается весьма несложно, т.к. надо, по сути, сравнить значения в соседних ячейках каждой строки. Как самый простой вариант — используем формулу для сравнения значений, выдающую на выходе логические значения ИСТИНА (TRUE) или ЛОЖЬ (FALSE):
Число несовпадений можно посчитать формулой:
=СУММПРОИЗВ(—(A2:A20<>B2:B20))
или в английском варианте =SUMPRODUCT(—(A2:A20<>B2:B20))
Если в результате получаем ноль — списки идентичны. В противном случае — в них есть различия. Формулу надо вводить как формулу массива, т.е. после ввода формулы в ячейку жать не на Enter, а на Ctrl+Shift+Enter.
Если с отличающимися ячейками надо что сделать, то подойдет другой быстрый способ: выделите оба столбца и нажмите клавишу F5, затем в открывшемся окне кнопку Выделить (Special) — Отличия по строкам (Row differences). В последних версиях Excel 2007/2010 можно также воспользоваться кнопкой Найти и выделить (Find & Select) — Выделение группы ячеек (Go to Special) на вкладке Главная (Home)
В последних версиях Excel 2007/2010 можно также воспользоваться кнопкой Найти и выделить (Find & Select) — Выделение группы ячеек (Go to Special) на вкладке Главная (Home)
Excel выделит ячейки, отличающиеся содержанием (по строкам). Затем их можно обработать, например:
- залить цветом или как-то еще визуально отформатировать
- очистить клавишей Delete
- заполнить сразу все одинаковым значением, введя его и нажав Ctrl+Enter
- удалить все строки с выделенными ячейками, используя команду Главная — Удалить — Удалить строки с листа (Home — Delete — Delete Rows)
- и т.д.
Вариант 2. Перемешанные списки
Если списки разного размера и не отсортированы (элементы идут в разном порядке), то придется идти другим путем.
Самое простое и быстрое решение: включить цветовое выделение отличий, используя условное форматирование.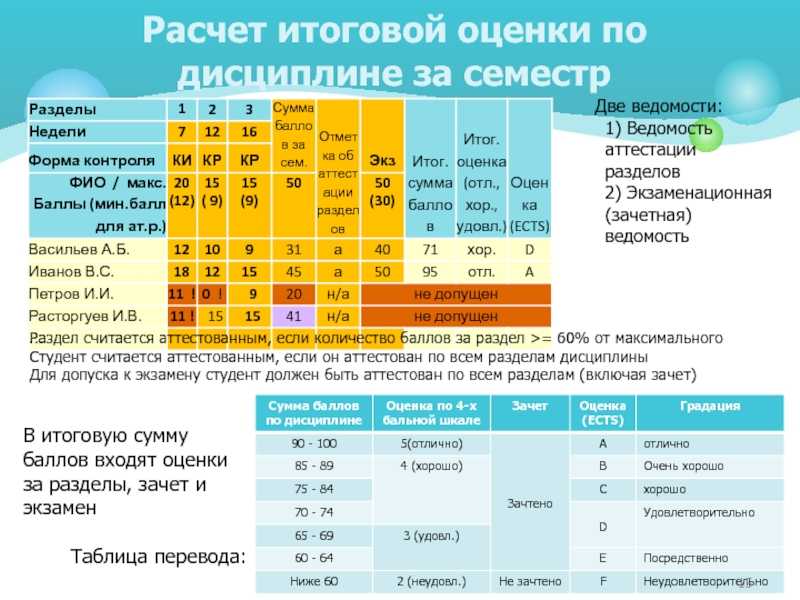 Выделите оба диапазона с данными и выберите на вкладке Главная — Условное форматирование — Правила выделения ячеек — Повторяющиеся значения (Home — Conditional formatting — Highlight cell rules — Duplicate Values):
Выделите оба диапазона с данными и выберите на вкладке Главная — Условное форматирование — Правила выделения ячеек — Повторяющиеся значения (Home — Conditional formatting — Highlight cell rules — Duplicate Values):
Если выбрать опцию Повторяющиеся, то Excel выделит цветом совпадения в наших списках, если опцию Уникальные — различия.
Цветовое выделение, однако, не всегда удобно, особенно для больших таблиц. Также, если внутри самих списков элементы могут повторяться, то этот способ не подойдет.
В качестве альтернативы можно использовать функцию СЧЁТЕСЛИ (COUNTIF) из категории Статистические, которая подсчитывает сколько раз каждый элемент из второго списка встречался в первом:
Полученный в результате ноль и говорит об отличиях.
И, наконец, «высший пилотаж» — можно вывести отличия отдельным списком. Для этого придется использовать формулу массива:
Выглядит страшновато, но свою работу выполняет отлично 😉
Ссылки по теме
- Выделение дубликатов в списке цветом
- Сравнение двух диапазонов с помощью надстройки PLEX
- Запрет ввода повторяющихся значений
Пропорция – принцип искусства
Пропорция – это принцип искусства, относящийся к относительному размеру. Принципы искусства отличаются от элементов искусства. Большинство, если не все принципы искусства касаются того, как элементы искусства расположены в произведении искусства.
Принципы искусства отличаются от элементов искусства. Большинство, если не все принципы искусства касаются того, как элементы искусства расположены в произведении искусства.
Пропорция в основном связана с соотношением размеров одного элемента по сравнению с другим. При реалистичном рисовании важны пропорции. Если пропорции неверны, то полученное изображение будет выглядеть менее реалистичным или абстрактным.
В качестве альтернативы художники могут использовать пропорции для эффекта. Управляя пропорциями, художник может сделать свой объект сильным, слабым, забавным, загадочным и т. д. Мы можем преувеличивать пропорции, чтобы подчеркнуть значение или элемент сцены. Например, карикатурист искажает пропорции, чтобы создать стилизованное изображение предмета.
Прежде чем идти дальше, давайте определим пропорции в изобразительном искусстве. Пропорция относится не к общему размеру, а скорее к соотношению размеров двух или более предметов или элементов. В искусстве размер элемента обозначается как шкала . Например, баскетбольный и бейсбольный мячи различаются по масштабу, но имеют одинаковые пропорции.
Например, баскетбольный и бейсбольный мячи различаются по масштабу, но имеют одинаковые пропорции.
Композиционная пропорция
На протяжении тысячелетий художники искали наиболее эстетичный способ расположения визуальных компонентов в композиции. От двухмерных произведений искусства до архитектуры художники ищут пропорции (соотношения), которые радуют глаз. Одна популярная концепция была открыта древнегреческим математиком Евклидом. Он назвал это соотношение Золотое сечение (Соотношение, выраженное в цифрах: 1,6180:1).
Золотую середину часто изображают как линию, разделенную в определенной точке. Линия разделена на два сегмента. Относительное отношение одной части равно ко второй части, а второй части равно ко всему – звучит запутанно, не так ли? Золотую середину лучше всего понять визуально (см. диаграмму ниже).
Чтобы объяснить, C относится к B, как B к A.
Евклид также применил это отношение к фигуре и назвал ее золотым прямоугольником.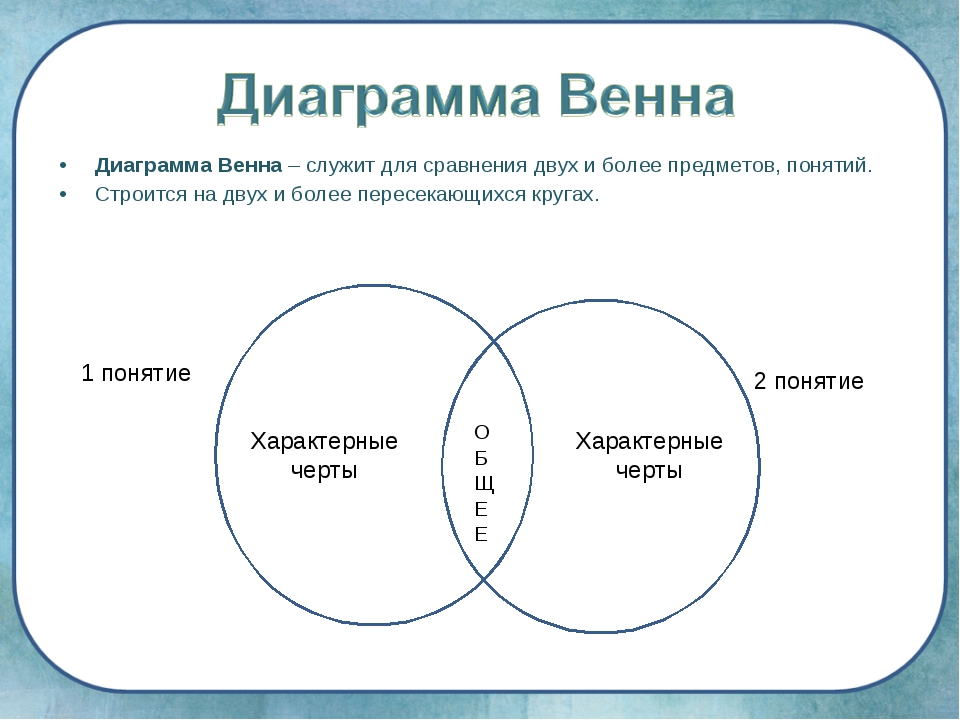 Как показывает иллюстрация, процесс деления прямоугольника на золотую середину повторяется бесконечно.
Как показывает иллюстрация, процесс деления прямоугольника на золотую середину повторяется бесконечно.
Художники использовали золотую середину, чтобы помочь им принять решение о размещении важных визуальных элементов — не только на картинах — но также определить размер и расстояние между архитектурными элементами.
Мы можем использовать золотую середину для создания визуально приятных произведений искусства, размещая важные предметы в соответствии с пропорциями в нашем искусстве.
Витрувианский человек
Золотая середина проявляется и в природе. В первом веке римский архитектор по имени Витрувий изучал пропорции. Он считал, что человеческое тело является эстетически лучшим образцом пропорции. Он применил человеческие пропорции к своим архитектурным проектам.
Опираясь на концепцию универсальных эстетических пропорций, Леонард да Винчи попытался проиллюстрировать идеальные пропорции человека, изложенные Витрувием за столетия до этого. Он назвал это «Витрувианским человеком».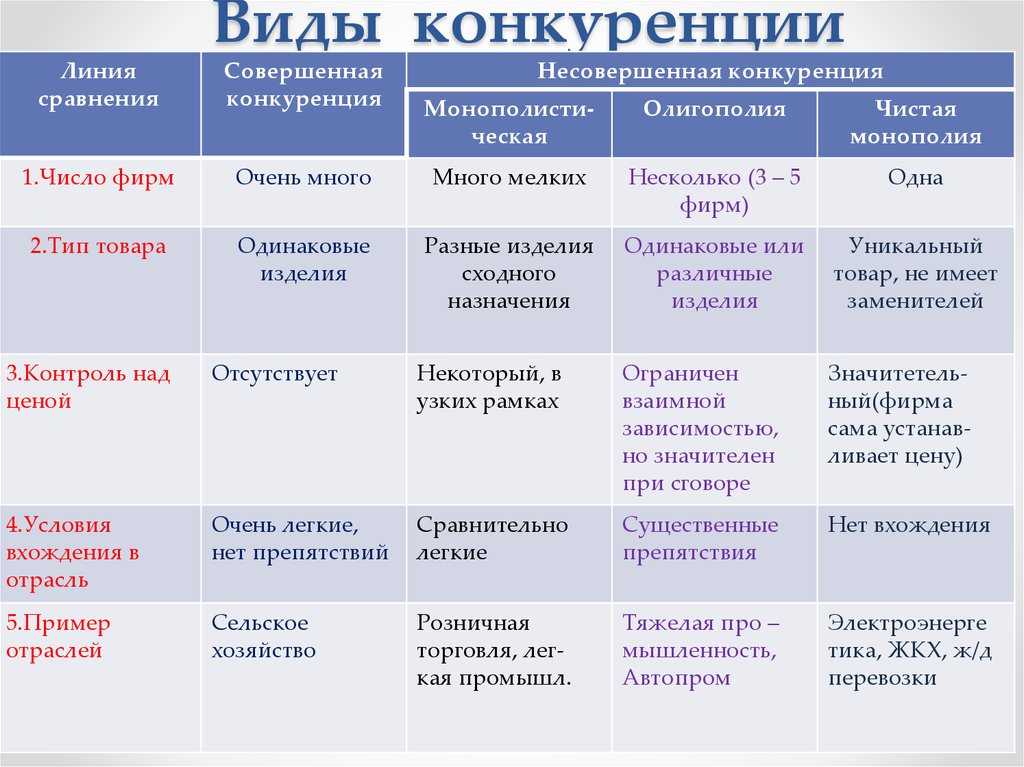
В то время художники считали, что если будет открыта и использована идеальная пропорция, то их искусство будет пользоваться особым преимуществом и приведет к определенному успеху.
Пропорции человеческого тела
Могут существовать или не существовать «идеальные» пропорции человеческого тела. Реалистичные пропорции человека попадают в узкий диапазон. Этот диапазон объясняет разнообразие наблюдаемых типов телосложения. Безусловно, длина рук, ног и туловища может сильно различаться, но пропорциональные вариации незначительны. У невысокого человека короткие руки и ноги, а у высокого человека длинные руки и ноги. Отношение длины рук к длине ног у обоих людей примерно одинаковое, хотя один из них высокий, а другой низкий.
В искусстве мы говорим о человеческих пропорциях по отношению к голове . Различия в размерах тела больше, чем различия в размерах головы среди людей. Среднее соотношение «роста к голове» для человека составляет семь с половиной к одному.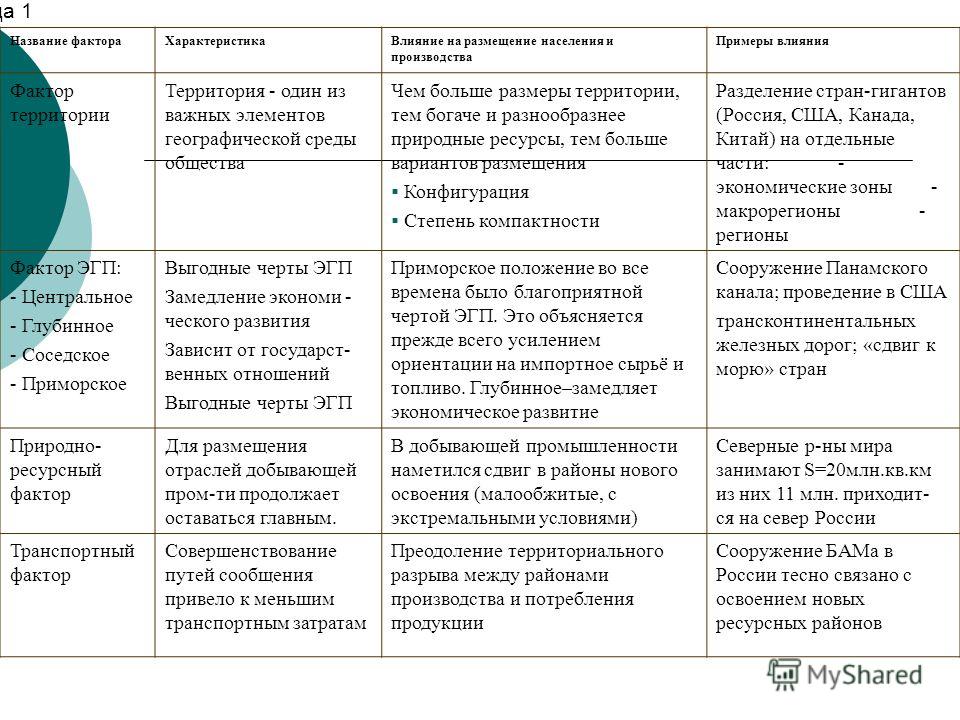 Это означает, что высота головы человека делится на его общий рост в среднем в 7,5 раз.
Это означает, что высота головы человека делится на его общий рост в среднем в 7,5 раз.
Каковы ваши пропорции? Измерьте свою голову от макушки до подбородка, а затем разделите полученное значение на общий рост. Например, мой рост 68 дюймов, а высота моей головы 9 дюймов. 68 разделить на 9 будет примерно 7,5. Мой рост 7,5 головы, средние человеческие пропорции.
См. также: Как быстро нарисовать фигуру человека — рисование жестами
Два человека могут быть одного роста и разных пропорций, так же как два человека могут быть разного роста, но иметь одинаковые пропорции. См. иллюстрацию ниже.
Пропорции человеческого лица
Знание средних пропорций человеческого лица полезно по двум причинам. Во-первых, знание средних пропорций помогает художнику избежать серьезных ошибок при работе с воображением. Во-вторых, средние пропорции служат отправной точкой, по которой можно судить о людях при захвате сходства. Чем мы отличаемся от «средних», это то, что делает нас узнаваемыми друг для друга.
Вот несколько обобщений, касающихся пропорций лица…
- Человеческая голова обычно больше в высоту, чем в ширину.
- Форма лица приблизительно симметрична относительно вертикальной оси.
- Глаза падают на воображаемую линию, которая горизонтально делит голову через центр.
- Нижняя часть носа пересекает вторую воображаемую линию между «линией глаз» и нижней частью подбородка.
- Рот ближе к носу, чем нижняя часть подбородка.
Кроме того, на лице средних пропорций расстояние между глазами равно ширине одного глаза. Ширина носа равна или немного шире, чем расстояние между глазами, а ширина рта равна ширине центра глаз. См. иллюстрацию ниже.
В профиль у среднего человека задняя часть уха находится на таком же расстоянии от внешнего угла глаза, как внешний угол глаза от нижней части подбородка.
См. также: Как нарисовать лицо. Основные пропорции головы
Нереалистичные пропорции
Иногда преувеличенные или искаженные пропорции намеренно используются для передачи определенного значения или сообщения.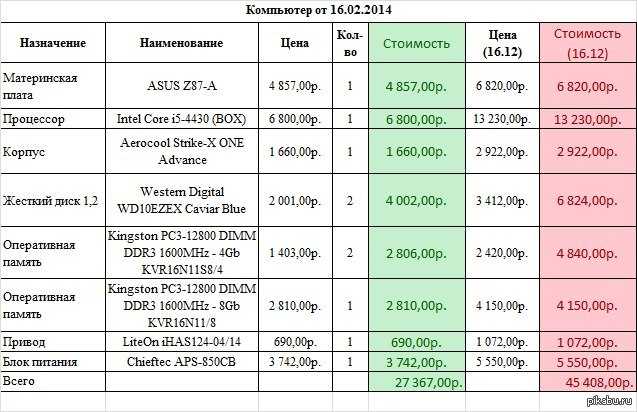 Расширяя, удлиняя, сжимая и изгибая части человеческого тела, художник может создать ощущение или настроение вокруг предмета. Давайте рассмотрим двух исторически известных художников и их соответствующие стили — Эль Греко и Пикассо.
Расширяя, удлиняя, сжимая и изгибая части человеческого тела, художник может создать ощущение или настроение вокруг предмета. Давайте рассмотрим двух исторически известных художников и их соответствующие стили — Эль Греко и Пикассо.
Эль Греко родился в Греции, жил и работал в Испании. Большая часть его произведений носит религиозный характер. Он предпочитал преувеличивать человеческую фигуру почти во всех своих картинах. Его методом преувеличения было удлинение. Эль Греко чувствовал, что, «растягивая» человеческую форму, он побуждал свою аудиторию смотреть вверх и думать о Боге. Его фигуры определенно тянулись к Небесам. Кроме того, удлиняя своих героев, Эль Греко придавал им потустороннее, духовное ощущение бытия.
Пикассо, также родом из Испании, работал в нескольких стилях и был пионером. В начале 1920-х он написал серию картин об отношениях матери и ребенка. В этой серии фигурки толстые и тяжелые на вид. Пикассо преувеличивал ширину тела по сравнению с головой, придавая своим фигурам устойчивое, скульптурное ощущение.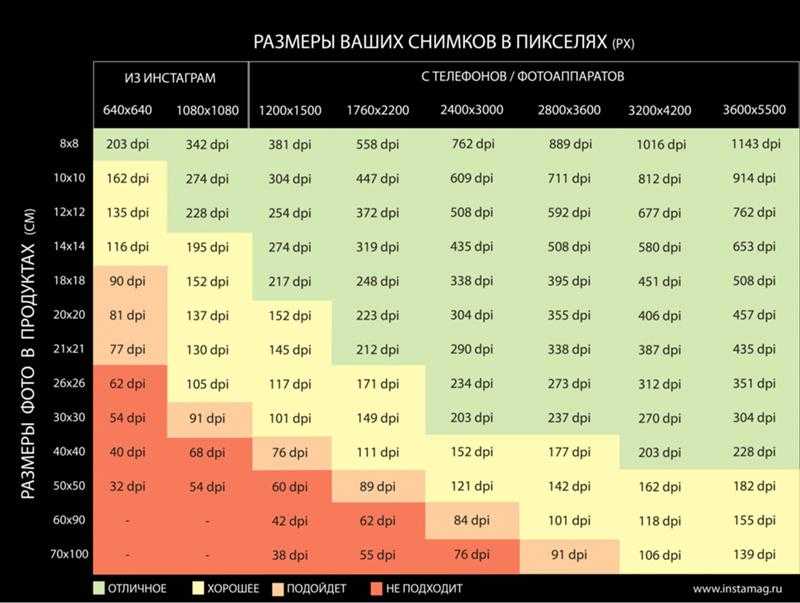 Это стабильное чувство свидетельствует о надежных, непоколебимых отношениях между матерью и ее ребенком — типе отношений, которые, как он надеялся, будут у его детей с их собственной матерью.
Это стабильное чувство свидетельствует о надежных, непоколебимых отношениях между матерью и ее ребенком — типе отношений, которые, как он надеялся, будут у его детей с их собственной матерью.
Заключение
Как художники, мы можем выбирать, использовать цвет или нет. Мы можем решить использовать ударение или нет. Однако ускользающей пропорции нет. Просто нельзя «выбросить». Пропорция – важный инструмент художника. С точными пропорциями мы можем создавать реалистичные рисунки и картины. Управляя пропорциями, мы можем подчеркивать элементы и передавать идеи. Пропорция — мощный принцип, который должен понять каждый художник.
Больше уроков, которые вам понравятся…
Рубрика: Рисование, Образование, Живопись
Правило размера ранга: определение, модель и примеры
Почему так много людей переезжают или живут в городе? Что замедляет рост города, когда он достигает определенного размера? Правило ранга-размера — это принцип, который может объяснить распределение некоторых городов. Этот принцип объясняет наблюдаемую во многих странах закономерность в отношении пределов и размеров городов, которые будут достигнуты в зависимости от их положения и относительной численности населения. В этом объяснении мы более подробно рассмотрим правило размера ранга.
Этот принцип объясняет наблюдаемую во многих странах закономерность в отношении пределов и размеров городов, которые будут достигнуты в зависимости от их положения и относительной численности населения. В этом объяснении мы более подробно рассмотрим правило размера ранга.
Определение правила размера ранга
Правило размера ранга — это правило об обратном размере ранга, часто описываемом как размер городов в стране. Правило размера ранга гласит, что второй по величине город будет иметь половину населения как самого большого. Третий по величине город будет иметь одну треть размера, а четвертый будет иметь одну четверть размера самого большого, и так далее и тому подобное. Другими словами, вы можете оценить численность населения города, основываясь на его ранге относительно крупнейшего города страны.
Правило размера ранга было вдохновлено Законом Ципфа , который используется в естественных и социальных науках для отражения обратной пропорциональности между вещами относительно их рангов.
Формула правила размера ранга
Конкретная формула правила размера ранга: 1/n th , где n соответствует рейтингу размера города в стране. Например, Лос-Анджелес, штат Калифорния, является вторым по величине городом в Соединенных Штатах. Следовательно, его ранг будет равен двум, а по формуле ранг-размер — 9.0009 n будет равняться двум.
Если мы знаем, какой ранг имеет город с точки зрения размера населения по сравнению с другими городами страны, мы можем затем увидеть, соответствует ли самый большой город соотношению, чтобы увидеть, следует ли страна правилу ранга-размера. Следовательно, размеры городов обратно пропорциональны их рангу.
Существуют аргументы в пользу того, что правило размера ранга является скорее статистическим явлением, чем законом или универсальной концепцией, потому что это правило иногда присутствует, но определенно непостоянно при рассмотрении распределения населения по городам в разных странах.
Хотя мы обычно говорим о городах с правилом размера ранга, оно может быть применимо и в более широком смысле. На приведенном ниже рисунке показано население стран, которые следуют схеме экспоненциальной обратной регрессии, как и следовало ожидать в соответствии с их рангом, основанным на правиле размера ранга. Китай и Индия являются аномалиями, но население любой другой страны близко соответствует ожидаемому населению.
Рис. 1. Распределение ранга по размеру
Пример правила размера ранга
Давайте посмотрим на размер разных городов в Соединенных Штатах. Нью-Йорк — крупнейший город США с населением около 8,5 млн человек.
Лос-Анджелес — второй по величине город США. В нашей формуле n = 2, и формула будет 1/2. Мы ожидаем, что население Лос-Анджелеса составит примерно половину, или 50%, населения Нью-Йорка. Население Лос-Анджелеса составляет 3,8 млн человек, что составляет около 44,7% населения Нью-Йорка. Это довольно близко к половине, но все же немного не так. В этом примере можно сказать, что применяется правило размера ранга, поскольку оно по-прежнему дает приблизительную оценку. 2
В этом примере можно сказать, что применяется правило размера ранга, поскольку оно по-прежнему дает приблизительную оценку. 2
NYC=8,5LA=3,88,52=4,254,25=50% от NYC3,88,5=0,447×100=44,7%
Посмотрим, сохранится ли эта тенденция в США.
Чикаго, третий по величине город США, имеет население около 2,7 млн человек. Следуя нашей формуле размера ранга, n будет равно трем, поэтому мы ожидаем, что население Чикаго составит примерно одну треть от 33% населения крупнейшего города страны, Нью-Йорка, с населением 8,5 миллионов человек. 2,7 миллиона — это примерно 32% от 8,5 миллиона, что почти соответствует правилу размера ранга.2
Рис. 2. Очертания Чикаго
Хьюстон, штат Техас, является вторым по численности населения городом в Соединенных Штатах, где проживает около 2,3 миллиона человек. Как четвертый по величине город в Соединенных Штатах, мы должны ожидать, что население Хьюстона составит одну четвертую или 25% населения Нью-Йорка, если он будет следовать правилу размера ранга. Размер Хьюстона примерно на 27 % меньше Нью-Йорка, что опять-таки близко к тому, что предсказывает правило размера ранга.2
Размер Хьюстона примерно на 27 % меньше Нью-Йорка, что опять-таки близко к тому, что предсказывает правило размера ранга.2
И последнее: пятым по величине городом в Соединенных Штатах является Феникс, штат Аризона.
Население Феникса составляет 1,6 миллиона человек. К настоящему времени вы должны знать, что пятый по величине город в Соединенных Штатах должен составлять примерно одну пятую или 20% от размера Нью-Йорка. Размер Феникса составляет примерно 19% от размера Нью-Йорка, что опять-таки довольно близко следует правилу размера ранга2.
Могут возникнуть разногласия по поводу границ города. Что, если мы сравним не только города, но и большие мегаполисы, чтобы посмотреть на разные измерения городского населения? Агломерация города намного больше, включая пригороды и населенные пункты в непосредственной близости от города, которые находятся в сильно зависимых отношениях с городом. Население мегаполиса Нью-Йорка составляет около 19 человек.0,8 миллиона человек, что более чем в два раза превышает количество людей, живущих в черте города. В столичном районе Лос-Анджелеса проживает около 13 миллионов человек. Агломерация Лос-Анджелеса составляет почти 65% площади агломерации Нью-Йорка. Что это может нам сказать? Что ж, правило размера ранга здесь не так сильно применимо, но Лос-Анджелес также может определять свою агломерацию иначе, чем Нью-Йорк. Известно, что в Лос-Анджелесе нет системы метро, его центр города не такой большой, а его население в целом более рассредоточено по большей части территории. Возможно, это приводит к более широкому определению мегаполиса в Лос-Анджелесе, чем в Нью-Йорке.
В столичном районе Лос-Анджелеса проживает около 13 миллионов человек. Агломерация Лос-Анджелеса составляет почти 65% площади агломерации Нью-Йорка. Что это может нам сказать? Что ж, правило размера ранга здесь не так сильно применимо, но Лос-Анджелес также может определять свою агломерацию иначе, чем Нью-Йорк. Известно, что в Лос-Анджелесе нет системы метро, его центр города не такой большой, а его население в целом более рассредоточено по большей части территории. Возможно, это приводит к более широкому определению мегаполиса в Лос-Анджелесе, чем в Нью-Йорке.
Модель правила размера ранга
Правило размера ранга может многое рассказать нам о стране. Это может показать нам, что страна имеет более высокий уровень развития и инклюзивных институтов, потому что власть и богатство распределены справедливо по сравнению с другими моделями. Быстрый рост, как это происходит во многих странах Азии, может затруднить соблюдение правила размера ранга, поскольку много власти и инвестиций сосредоточено в одном городе, и прошло недостаточно времени, чтобы урбанизация и развитие распространились на всю страну.
Правило размера ранга, как правило, работает лучше в странах, где на протяжении многих веков проживало большое городское население, так как это дает много времени для распространения урбанизации.
Ознакомьтесь с нашим объяснением теории центрального места!
Правило рангового размера в сравнении с городом-приматом
Правило рангового размера описывает убывающий порядок прогрессивно меньших, но независимо функционирующих городов, тогда как город-примат является в подавляющем большинстве случаев самым большим городом в стране и центром большей части промышленности, власти, и общественные тенденции. Если в стране есть только один крупный город-примат, а не набор городов, которые следуют правилу размера ранга, это может означать, что страна находится на 9-м месте.0063 менее устойчивый; город приматов может иметь пагубное влияние на остальную часть страны, в то время как власть и богатство более распространены в странах, следующих правилу размера ранга.
Примером страны с городом-приматом может быть Таиланд, поскольку Бангкок на сегодняшний день является крупнейшим мегаполисом, а следующий по величине городской район более чем в 30 раз меньше. Города-приматы часто являются менее желательной моделью, чем правило размера ранга, поскольку города-приматы обычно являются отражением или причиной неравенства, неравномерного развития и отсутствия справедливости. В провинциях вокруг Бангкока ВВП на душу населения может быть в 8-10 раз выше, чем во многих сельских провинциях Таиланда. 4
Рис. 3. Очертания Бангкока
Города-приматы, как правило, находятся в странах, которые развиваются и переживают быстрый экономический рост, или в странах, которые имеют долгую историю неравенства и авторитарного правления, сосредоточившего богатство в руках несколько, часто в центре политической власти. Однако это не всегда так, и авторитарные страны также могут следовать правилу размера ранга.
Ранг Размер Правило Сильные и слабые стороны
Достоинств правила размера ранга много. Большинство стран, которые следуют правилу ранжирования, в целом являются более сильными и более развитыми странами с долгой историей урбанизации , более равномерным развитием и меньшим неравенством. Страна будет более устойчивой и безопасной при наличии множества крупных городов, поскольку не все они вкладывают большую часть своих ресурсов и богатств в один город.
Большинство стран, которые следуют правилу ранжирования, в целом являются более сильными и более развитыми странами с долгой историей урбанизации , более равномерным развитием и меньшим неравенством. Страна будет более устойчивой и безопасной при наличии множества крупных городов, поскольку не все они вкладывают большую часть своих ресурсов и богатств в один город.
Некоторыми недостатками может быть отсутствие единого определения того, где именно должен заканчиваться и начинаться город, что почти позволяет корректировать границы города в соответствии с правилом. Еще одним недостатком может быть то, что это грубая оценка размеров городов, и при работе с большими странами это может означать, что измерение будет ошибочным на несколько сотен тысяч человек. Наконец, правило размера ранга лишь иногда применимо к некоторым странам, поскольку вместо этого во многих странах есть города-приматы; следовательно, было бы неверным предполагать размер других городов в любой данной стране только потому, что вы знаете ранг и размер одного города.
Правило размера ранга – основные выводы
- Правило размера ранга не является точным или универсальным измерением распределения населения в стране, но представляет собой принцип, отображающий закономерность, которую можно наблюдать во многих странах.
- Чем выше ранг города, тем меньше ожидаемая численность населения.
- Правило размера ранга — одна из нескольких теорий, описывающих распределение популяций.
- Правило ранга-размера является образцом пропорциональности.
Ссылки
- Рис. 1: Рейтинг населения страны (https://commons.wikimedia.org/wiki/File:Rank_order_countries.png) по Loodong (https://commons.wikimedia.org/wiki/User :Loodog) имеет лицензию CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0/deed.en)
- Бюро переписи населения США. «Общие данные о населении городов: 2020–2021 гг. “ https://www.census.gov/data/tables/time-series/demo/popest/2020s-total-cities-and-towns.html 16, май 2022 г.